прошлое.рф -
купить или арендовать доменное имя онлайн- Домены совпадающие с прошлое
- Покупка
- Аренда
- прошлое.рф
- 88 000
- 880
- Домены с синонимами прошлое
- Покупка
- Аренда
- былое.рф
- 88 000
- 880
- судимости.рф
- 100 000
- 1 000
- Флешбэк.рф
- 70 000
- 700
- Домены с переводом прошлое
- Покупка
- Аренда
- гасторы.рф
- 100 000
- 1 000
- пасти.рф
- 50 000
- 500
- пасы.рф
- 100 000
- 1 000
- Пцт.рф
- 60 000
- 600
- ретроспектива.рф
- 50 000
- 500
- хипстеры.рф
- 150 000
- 1 500
- хостеры.рф
- 110 000
- 1 100
- Домены начинающиеся с прошл
- Покупка
- Аренда
- прошлая.рф
- 88 000
- 880
- Домены с синонимами, содержащими прошл
- Покупка
- Аренда
- anamnez.ru
- 100 000
- 1 000
- Анамнезы.рф
- 70 000
- 700
- минувшее.рф
- 150 000
- 1 500
- отследим.рф
- 100 000
- 1 000
- последнее.рф
- договорная
- договорная
- последние.рф
- 100 000
- 1 000
- последний.рф
- 88 000
- 880
- проследим.рф
- 70 000
- 700
- ушедшие.рф
- 88 000
- 880
- Домены с переводом, содержащими прошл
- Покупка
- Аренда
- hlest.ru
- 70 000
- 700
- клац.рф
- 50 000
- 1 000
- хлыст.рф
- 88 000
- 880
- Энергичный выбор: Почему доменное имя электрическое.рф это ключ к электронному успеху и стабильному присутствию в Интернете
- Узнайте, как покупка или аренда доменного имени 'электрическое.рф' может повысить аудиторию и доверие к вашей электроэнергетической компании, делая ваш бренд легкоузнаваемым и устойчивым на российском рынке.
- Эксклюзивный домен щ1.рф: Почему он станет визитной карточкой вашего бизнеса
- Погрузитесь в цифровой мир России с доменным именем щ1.рф – идеальным выбором для создания узнаваемого онлайн-бренда и обеспечения эффективного продвижения вашего бизнеса в регионе.
- Электрокультиватор.РФ: Революция в сельхозтехнике – научиться побеждать природу прогрессом
- Электрокультиватор.РФ - революционное решение для сельского хозяйства, внедряющее энергосберегающие технологии и повышающее производительность труда, обеспечивая прогресс в ведении современного аграрного бизнеса.
- Шмотьё.рф: Тренды и Стильные Находки для Интернет-Магазина Одежды и Аксессуаров
- Шмотьё.рф – это инфоповод для владельцев интернет-магазинов одежды и аксессуаров, предлагающий современные тренды и стильные находки, чтобы выразить неповторимый стиль и бренд для ваших клиентов.
- Школьная.рф: Современные Учителя и Учебники - Революция в Образовании
- Откройте для себя Школьная.рф – надежный помощник современных учителей и учебников, предлагающий передовые решения для качественного образования и успешной учебы.
- Покупка и Аренда Домена шейпинг.рф: Инвестиции для Будущего Вашего Бизнеса
- Оптимизируй свой бизнес и инвестируй в будущее, выбирая наиболее подходящий альтернативный домен .шейпинг.рф – как путем покупки, так и аренды!
- Доменное имя чертов.рф: Преимущества покупки или аренды для вашего бизнеса
- Узнайте о преимуществах обладания уникальным доменным именем чертов.рф: повышает доверие к вашему веб-проекту и упрощает навигацию для пользователей, что приносит больший трафик и повышает конверсию на вашем сайте.
- Доменное имя цыпуля.рф: Лучший выбор для вашего бизнеса или проекта
- Оцените преимущества обладания уникальным доменным именем цыпуля.рф для вашего бизнеса – повысьте доверие клиентов, укрепляйте статус бренда и получайте выгоду от надежной локализации ресурса в сети.
- Доменное имя цель.su: Ваш ключ к успеху в интернет-бизнесе Развернутый ответ: Доменное имя является одним из основных инструментов в стратегии интернет-маркетинга, особенно при создании или продвижении онлайн-бизнеса. Одним из привлекательных вариантов до
- Узнайте, почему выбор доменного имени цель.su для вашего сайта обеспечит региону РФ актуальность и доверие, а аренда или покупка - гибкие пути к успешной интернет-деятельности.
- Заголовок статьи: 6 убедительных причин купить или арендовать доменное имя целуйся.рф
- Ознакомьтесь с преимуществами обладания уникальным доменным именем 'целуйся.рф', которое гарантирует запоминаемость, привлечение целевой аудитории и укрепление онлайн-присутствия на российском сегменте Интернета.
- Доменное имя честных.рф: Этика аренды и безопасная покупка для устойчивого онлайн-присутствия
- Доменное имя честных.рф - это надёжный выбор для совершения безопасных интернет-транзакций и этичного арендования, который гарантирует устойчивый и прозрачный интернет-статус для вашего бизнеса.
- Циферблат.рф: Инновационные инструменты для успешного ведения бизнеса и проектов
- Узнайте, как Циферблат.рф, передовая платформа управления прогрессом, становится неотъемлемым инструментом для эффективного ведения бизнеса и успешного развития проектов, обеспечивая прозрачность и контроль над каждым шагом на пути к достижению целей.
- Заказать доменное имя целофанчик.рф: Решаем вашу уникальность и преимущества аренды в интернете
- Заказывай доменное имя целофанчик.рф - ключ к пиару, уникальности и лучшему SEO эффекту для вашего онлайн-представительства на нашем специализированном сайте, где доступны варианты покупки и аренды.
- Инвестируйте в цифровое будущее: Почему выгодно приобретать или арендовать доменное имя Чоботы.рф
- Откройте доступ к успеху в цифровом пространстве с Чоботы.рф - доверенным доменом, гарантирующим узнаваемость бренда и перспективный экономический потенциал.
- Добро пожаловать на Черту! Черный Ренессанс - Возрождение Русской Культуры в домене .РФ
- Обзор на сайт домена .рф, где оживает русская культура и дается уникальный шанс окунуться в возрождение родной культуры в самом сердце Рунета.
- Добавление домена цельные.рф в ваш бизнес: Выгоды от покупки и аренды
- Узнайте, как интеграция домена <<цельные.рф>> в ваш бизнес может повысить доверие клиентов, улучшить SEO и усилить бренд, а также сравните преимущества покупки и аренды для вашей стратегии онлайн-присутствия.
- Хитрый.рф: Почему аренда или покупка домена - ваш ключ к успеху в интернете
- Узнайте о неоспоримых преимуществах и стратегической важности приобретения или аренды уникального доменного имени 'хитрый.рф' для укрепления онлайн-присутствия и привлечения целевой аудитории.
- Доменное имя Фрикасе.рф: Ваш ключ к успеху в сети Интернет
- Добавьте серьезности и профессионализма своему проекту, выбрав доменное имя фрикасе.рф для аренды или покупки, гарантируя узнаваемость, лояльность аудитории и позитивный имидж вашего бизнеса в интернете.
- Почему Фотоэлемент.рф – Ваш Шанс Взять Ворота Фотоиндустрии в России
- Откройте для себя истинную ценность владения доменом photoelement.rf и как аренда такого зонта может стать ключом к успешным онлайн-проектам в мире профессиональной фотографии.
- Аренда или Покупка Домена фикции.рф: 5 Непреодолимых Аргументов
- Изучи причины, почему приобретение или аренда доменного имени .рф для вашей вымышленной компании гарантирует локальное присутствие и повышение доверия клиентов, усиление бренда и выгодное сходство с известными фирмами.
- Ухта – центр Северного края: почему выгодно арендовать или купить доменное имя ухи.рф
- Активизируйте свой бизнес в интернете с помощью доменного имени ухи.рф – надёжной и привлекательной ссылки, гарантирующей расширение клиентской базы и повышение доверия к вашему бренду на российском рынке.
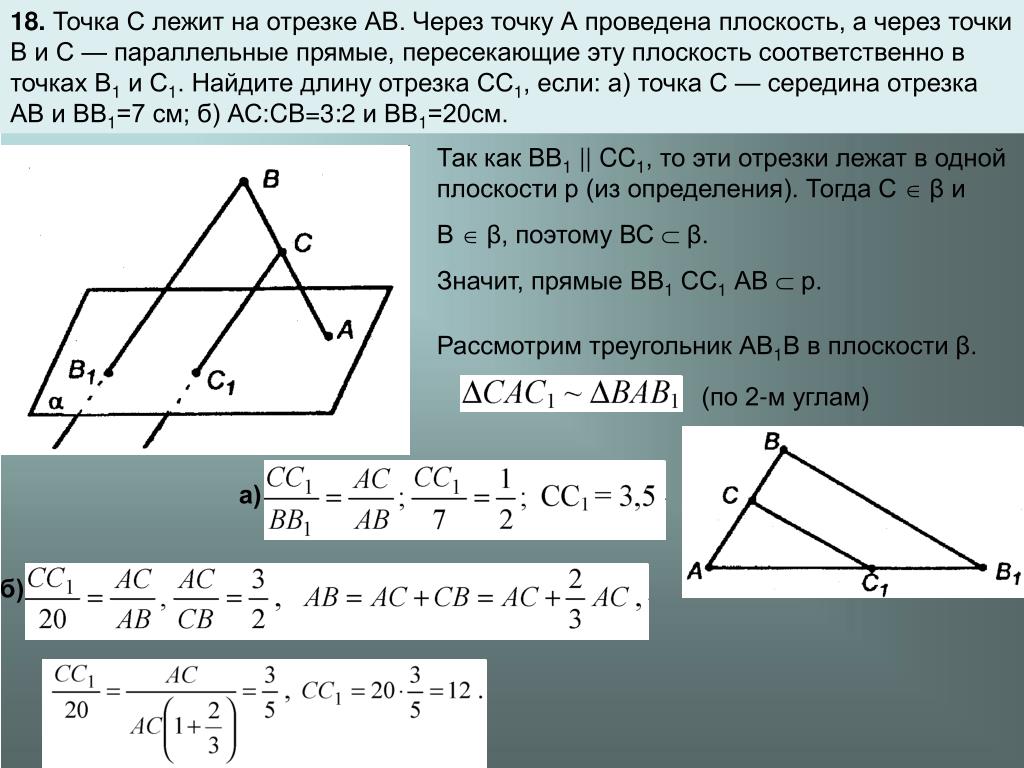
Точка расположена на отрезке, плоскость проходит через нее и параллельна двум данным прямым
Для начала, рассмотрим что такое точка с на отрезке ав. Это означает, что данная точка с лежит на отрезке, соединяющем две заданные точки а и в. Точка с находится между точками а и в и делит отрезок ав на две части в определенном отношении. Чтобы определить положение точки с на отрезке ав, мы можем использовать формулу нахождения координат точки по формуле с = (а + в)/2. Здесь а и в - координаты заданных точек, а с - координаты искомой точки с. Когда мы рассмотрим построение параллельных прямых в плоскости а через точки а и с, мы должны помнить о следующем. Для конструирования параллельной прямой, достаточно найти ее уравнение и использовать его для построения данной прямой. В данном случае мы знаем координаты точек а и с, и можем использовать эти данные для нахождения уравнения параллельной прямой. Что такое точка с на отрезке ав?Точка С на отрезке АВ играет важную роль в геометрии и математике в целом. Она позволяет решать различные задачи, связанные с расположением точек и отрезков в пространстве. Кроме того, точка С на отрезке АВ может использоваться для построения параллельных прямых в плоскости А, проходящих через точки А и С. Это свойство точки С помогает решать задачи по определению и построению параллельных линий и поверхностей.
Основные понятия и определенияПеред тем, как перейти к изучению точки с на отрезке ав и параллельных прямых в плоскости а через точки а и с, полезно разобраться в некоторых основных понятиях.
Знание этих основных понятий и определений поможет нам лучше понять тему точки с на отрезке ав и параллельных прямых в плоскости а через точки а и с и успешно продолжить изучение данной темы. Как найти точку с на отрезке ав?Чтобы найти точку С на отрезке АВ, нам понадобятся координаты точек А и В. Представим отрезок АВ в виде прямой, проходящей через эти две точки. Для нахождения точки С, которая будет лежать на этой прямой и параллельна другой прямой в плоскости А, используем формулу: С(xС, yС) = A(xA, yA) + t * (B(xB, yB) - A(xA, yA)) Здесь t – параметр, принадлежащий отрезку [0, 1]. Если t = 0, то точка С будет совпадать с точкой А, если t = 1 – с точкой В. Итак, мы знаем координаты точек А и В, а также значения параметра t. Подставляем все это в формулу и получаем координаты точки С. Пример:
Пусть А(2, 3) и В(6, 9). Находим значений параметра t, например, t = 0.5. С(xС, yС) = A(xA, yA) + t * (B(xB, yB) - A(xA, yA)) С(xС, yС) = (2, 3) + 0.5 * ((6, 9) - (2, 3)) С(xС, yС) = (2, 3) + 0.5 * (4, 6) С(xС, yС) = (2, 3) + (2, 3) С(xС, yС) = (4, 6) Таким образом, точка С находится на середине отрезка АВ и имеет координаты (4, 6). Существование и уникальность точки CДля того чтобы точка C существовала на отрезке AB и была параллельна прямым в плоскости, проходящим через точки A и B, необходимо выполнение определенных условий. Во-первых, для существования точки C на отрезке AB необходимо, чтобы точка A не совпадала с точкой B, иначе отрезок будет вырожденным. Во-вторых, чтобы точка C была параллельна прямым, нужно убедиться, что отрезок AB и прямые в плоскости, проходящие через точки A и B, действительно параллельны. Это означает, что угол между отрезком AB и любой из этих прямых должен быть равен 180 градусам. Если все условия выполнены, то точка C существует и является уникальной на отрезке AB, параллельна прямым в плоскости, проходящим через точки A и B. Параллельные прямые в плоскости а
Если две прямые параллельны, то их наклоны равны. Наклон прямой определяется через разность координат точек, через которые проходит прямая. Например, если прямая проходит через точки (х1, у1) и (х2, у2), то наклон прямой равен: м = (у2 - у1) / (х2 - х1). Если наклоны двух прямых равны, то они параллельны. И наоборот, если две прямые параллельны, то их наклоны равны. Кроме определения параллельности через наклоны прямых, можно использовать еще один способ - построение плоскости а. Для этого необходимо провести прямую через две точки a и с, а затем, провести скрещивающую прямую через точку a, параллельную прямой о. Если эти две прямые не пересекаются, то прямая о и параллельна прямой в плоскости а.
Уравнения прямых о и а имеют одинаковую функцию (2х), поэтому их наклоны равны и они параллельны. Как найти параллельные прямые через точки а и с?Для того чтобы найти параллельные прямые, проходящие через заданные точки A и C на плоскости, необходимо выполнить следующие шаги: Шаг 1: Определите координаты точек A и C. Для этого вам понадобятся значения x и y для каждой из точек. Шаг 2: Определите уравнение прямой, проходящей через точку A. Для этого можно использовать формулу наклона прямой, которая выглядит следующим образом: y - y1 = m(x - x1), где m - наклон прямой, а (x1, y1) - координаты точки A. Шаг 3: Используя полученное уравнение, подставьте координаты точки C и решите полученное уравнение относительно переменной m. Таким образом, вы сможете определить наклон параллельной прямой. Шаг 4: Найдите уравнение параллельной прямой, проходящей через точку C, используя найденный наклон m и координаты точки C. Вы можете использовать формулу y - y1 = m(x - x1), где (x1, y1) - координаты точки C. Шаг 5: Проверьте полученное уравнение, подставив в него координаты точек A и C. Если оба значения равны, значит, прямая, построенная по уравнению, параллельна прямой, проходящей через заданные точки A и C. Таким образом, следуя этим шагам, вы сможете найти параллельные прямые, проходящие через заданные точки A и C на плоскости. Статья рассказывает о плоскости, проходящей через точку А и параллельной прямым АВ и АС, лежащими на отрезке АВ. Точка с на отрезке ав и параллельные прямые в плоскости а через точки а и с Статья рассказывает о плоскости, проходящей через точку А и параллельной прямым АВ и АС, лежащими на отрезке АВ.
|

 Понимание понятия точка с на отрезке ав и параллельные прямые является важным элементом в изучении геометрии и математики в целом. В данной статье мы рассмотрим основные принципы и правила для определения точки с на отрезке ав и построения параллельных прямых в плоскости а через заданные точки а и с.
Понимание понятия точка с на отрезке ав и параллельные прямые является важным элементом в изучении геометрии и математики в целом. В данной статье мы рассмотрим основные принципы и правила для определения точки с на отрезке ав и построения параллельных прямых в плоскости а через заданные точки а и с.